Coastline Paradox

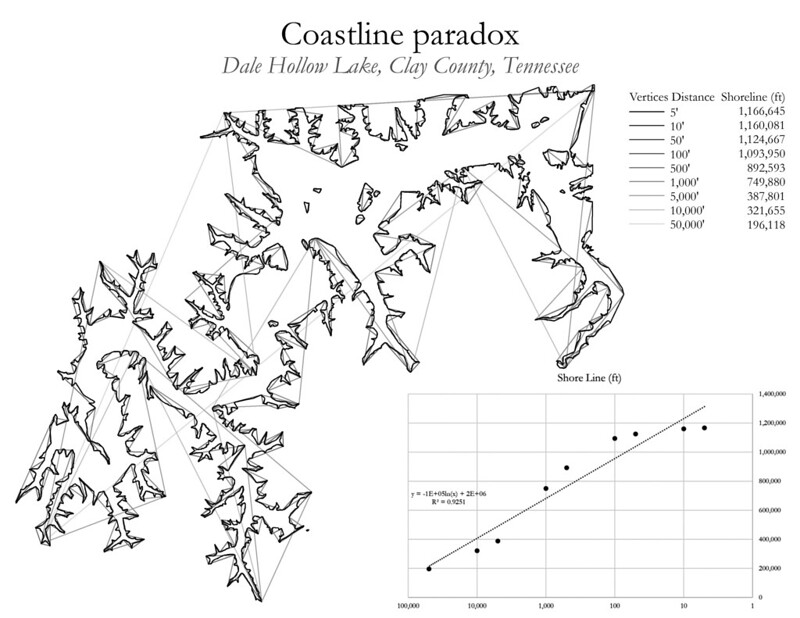
Coastline Paradox: Dale Hollow Lake, Clay County, Tennessee

Mandelbrot fractal Sunset Marina, Dale Hollow Lake, Pickett County, Tennessee 2 A coastline or a shoreline is something that can only be measured with a measurable degree of accuracy. As the measure of accuracy changes, so does the length of the coastline / shoreline. In other words, if I take a yardstick, a ruler, and 30' length of rope to measure the shore, I get three different answers. Each is correct, when stated with what was used to make the measurement.

This is a counterintuitive outcome. Geographic Information Systems (GIS) should be able to quite easily measure the length of lines, right?

The problem lies within the analysis itself. I can only tell where the shoreline of Dale Hollow Lake is based on known described layers of data with measured limitations. If I artificially inflate those limitations (in this example, I'm increasing distance between vertices) and record the change in shoreline, one can see how the shoreline decreases as the measure of accuracy decreases (distance between vertices increases, shoreline decreases). Same is true in reverse. As my measures get more accurate (smaller vertices), the shoreline length will continue to increase. This could be done all the way down to Planck scale (I think) where its length begins to approach infinity. This is due to the fractal nature of reality.

Look carefully at the above image. If you take the most detailed version of the lake and realize that if you continue to zoom in, you will continue to see that same pattern emerging as you peer ever closer. Mandelbrot created his famous fractal to describe this exact thing.

At Planck scale (and even well before) errors are introduced regarding the lakes elevation, which itself fluctuates, and is also subject to gravitational changes as well as aeolian alteration.

In short, one can only measure something with so much accuracy. How much is that? I have no idea.

For more reading: en.wikipedia.org/wiki/Coastline_paradox

Comments

Post a Comment

Popular posts from this blog

Missing People Map

Image
Sometime around middle to late November of 2019, I started getting tagged in posts on Reddit and Facebook where a map purported to show a correlation between missing person cases and caves. The two maps in question were of terrible quality in both content and image quality (so very much JPG compression). Somehow these maps managed to capture the public's attention for several weeks. In fact, more than two months later I am still being asked questions about the map. What follows is a critical analysis of the maps from both a cartographer's perspective, as well as a caver's. Origin Where did each image come from that comprised the map? The top image is titled " North America Cluster Map " and is produced by the Canam Missing Project / Missing 411. I cannot comment on the methods used to produce the map since they aren't stated. For this reason I am immediately suspect that this is conveying real information. I'll touch on why the form of this ma
Read more

Streams of Tennessee

Image
Longest Stream Segments Between Confluences All of the longest stream segments between confluences occur in areas of karst topography, interestingly enough. The implication is that there are actually other streams and confluences, but are underground as cave streams and springs, neither of which would appear in the National Hydrographic Dataset. Part of this 1) Calfkiller River†, White County , 12.12 miles 2) Collins River, Warren County , 10.69 miles 3) Falling Water River, Putnam & White County , 10.59 miles 4) Blackwater Creek, Hancock County , 10.23 miles 5) Duck River, Maury & Marshall County , 10.12 miles 6) Big Sycamore Creek, Claiborne & Hancock County , 10.03 miles 7) Hurricane Creek, Rutherford & Wilson County , 10.02 miles 8) Happy Creek, Sevier County , 9.53 miles 9) East Rock Creek, Marshall County , 8.82 miles 10) War Creek, Hawkins County , 8.56 miles †Calfkiller River is more likely 13.23 miles since the "confluence" measured
Read more

Jungle Book Film (1994) and the Upper Cumberland

Image
Table of Contents The Story David Starnes's Photos April Moore's Photos Watch Guide for Locals THE STORY BEHIND WALT DISNEY'S DECISION TO FILM RUDYARD KIPLING'S JUNGLE BOOK MOVIE AT LOST CREEK CAVE AND WATERFALL A PERSONAL RECOLLECTION BY DAVID STARNES RETIRED PRINCIPAL PLANNER LOCAL PLANNING ASSISTANCE OFFICE TENNESSEE DEPARTMENT OF ECONOMIC AND COMMUNITY DEVELOPMENT I was employed by the State of Tennessee as a community planner from October 1990 to August 2011. The Local Planning Assistance Office of the Upper Cumberland region was based in Cookeville. Our agency was in the Tennessee Department of Economic and Community Development, which also included the Tennessee Film Commission. Occasionally, different agencies would meet to explain their role in fostering economic growth in the state, and this was how my love for caving became entwined in the 1994 Walt Disney live-actio
Read more